3. Trigonometry
e. Inverse Trig Functions
4. Inverse Secant & Cosecant
Arc Secant
The secant function is not one-to-one, since for example \[ \sec(-\theta)=\sec(\theta) \] We pick the branch with \(0 \le \theta \lt \dfrac{\pi}{2}\) or \(\dfrac{\pi}{2} \lt \theta \le \pi\).
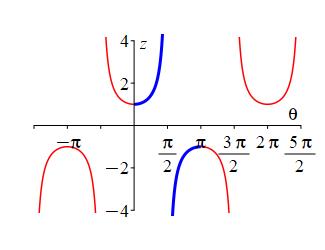
The inverse function of \(\sec\) is \(\text{arcsec}\) (read “arc secant”) or \(\sec^{-1}\) (read “inverse secant”) which satisfies \[ \text{arcsec}(z)=\theta \qquad \text{where} \qquad z=\sec(\theta) \] provided \(|z| \ge 1\) and \(0 \le \theta \lt \dfrac{\pi}{2}\) or \(\dfrac{\pi}{2} \lt \theta \le \pi\).
Notice that \(0 \le \theta \lt \dfrac{\pi}{2}\) or \(\dfrac{\pi}{2} \lt \theta \le \pi\) is quadrants I and II only but not the \(y\)-axis.
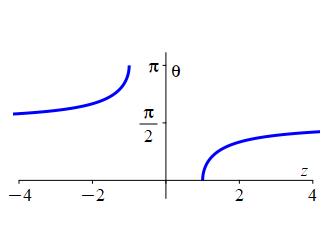
Compute each of the following.
-
\(\text{arcsec}\,2\)
\(\text{arcsec}\,2=\dfrac{\pi}{3}\)
-
\(\text{arcsec}(-\sqrt{2})\)
\(\text{arcsec}(-\sqrt{2})=\dfrac{3\pi}{4}\)
-
\(\text{arcsec}\,\dfrac{2}{\sqrt{3}}\)
\(\text{arcsec}\,\dfrac{2}{\sqrt{3}}=\dfrac{\pi}{6}\)
-
\(\text{arcsec}(-1)\)
\(\text{arcsec}(-1)=\pi\)
Arc Cosecant
The cosecant function is not one-to-one, since for example \[ \csc(\pi-\theta)=\csc(\theta) \] We pick the branch with \(-\,\dfrac{\pi}{2} \le \theta \lt 0\) or \(0 \lt \theta \le \dfrac{\pi}{2}\).
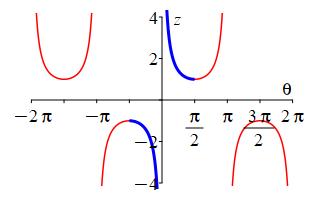
The inverse function of \(\csc\) is \(\text{arccsc}\) (read “arc cosecant”) or \(\csc^{-1}\) (read “inverse cosecant”) which satisfies \[ \text{arccsc}(z)=\theta \qquad \text{where} \qquad z=\csc(\theta) \] provided \(|z| \ge 1\) and \(-\,\dfrac{\pi}{2} \le \theta \lt 0\) or \(0 \lt \theta \le \dfrac{\pi}{2}\).
Notice that \(-\,\dfrac{\pi}{2} \le \theta \lt 0\) or \(0 \lt \theta \le \dfrac{\pi}{2}\) is quadrants IV and I only but not the \(x\)-axis.
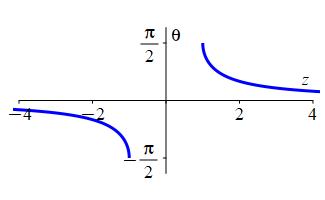
Compute each of the following.
-
\(\text{arccsc}\,2\)
\(\text{arccsc}\,2=\dfrac{\pi}{6}\)
-
\(\text{arccsc}(-\sqrt{2})\)
\(\text{arccsc}(-\sqrt{2})=-\,\dfrac{\pi}{4}\)
-
\(\text{arccsc}\,\dfrac{2}{\sqrt{3}}\)
\(\text{arccsc}\,\dfrac{2}{\sqrt{3}}=\dfrac{\pi}{3}\)
-
\(\text{arccsc}(-1)\)
\(\text{arccsc}(-1)=-\,\dfrac{\pi}{2}\)
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum